Electrical resonance
Electrical resonance occurs in an electric circuit at a particular resonance frequency where the imaginary parts of circuit element impedances or admittances cancel each other. In some circuits this happens when the impedance between the input and output of the circuit is almost zero and the transfer function is close to one.
Resonant circuits exhibit ringing and can generate higher voltages and currents than are fed into them. They are widely used in wireless (radio) transmission for both transmission and reception.
Resonance in LC circuits
Resonance of a circuit involving capacitors and inductors occurs because the collapsing magnetic field of the inductor generates an electric current in its windings that charges the capacitor, and then the discharging capacitor provides an electric current that builds the magnetic field in the inductor. This process is repeated continually. An analogy is a mechanical pendulum.
At resonance, the series impedance of the two elements is at a minimum and the parallel impedance is at maximum. Resonance is used for tuning and filtering, because it occurs at a particular frequency for given values of inductance and capacitance. It can be detrimental to the operation of communications circuits by causing unwanted sustained and transient oscillations that may cause noise, signal distortion, and damage to circuit elements.
Parallel resonance or near-to-resonance circuits can be used to prevent the waste of electrical energy, which would otherwise occur while the inductor built its field or the capacitor charged and discharged. As an example, asynchronous motors waste inductive current while synchronous ones waste capacitive current. The use of the two types in parallel makes the inductor feed the capacitor, and vice versa, maintaining the same resonant current in the circuit, and converting all the current into useful work.
Since the inductive reactance and the capacitive reactance are of equal magnitude, ωL = 1/ωC, so:
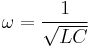
where ω = 2πf, in which f is the resonance frequency in hertz, L is the inductance in henries, and C is the capacitance in farads when standard SI units are used.
The quality of the resonance (how long it will ring when excited) is determined by its Q factor, which is a function of resistance.
See also
- Antiresonance
- Antenna theory
- Cavity resonator
- Electronic oscillator
- Resonance
- RLC circuit
- Electronic filter
- Resonant energy transfer - wireless energy transmission between two resonant coils
References
This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".